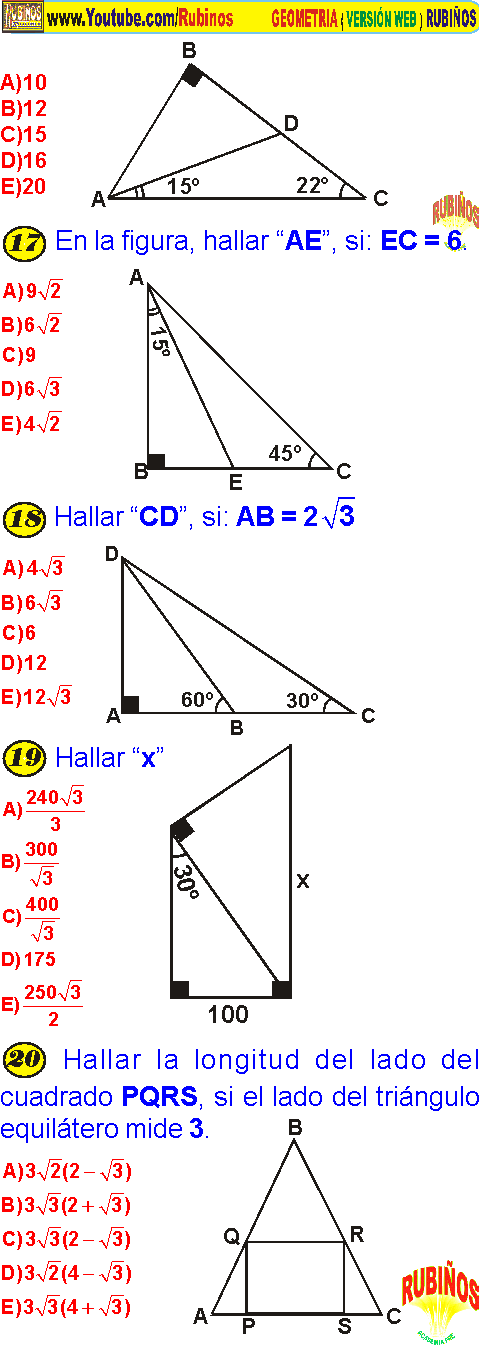
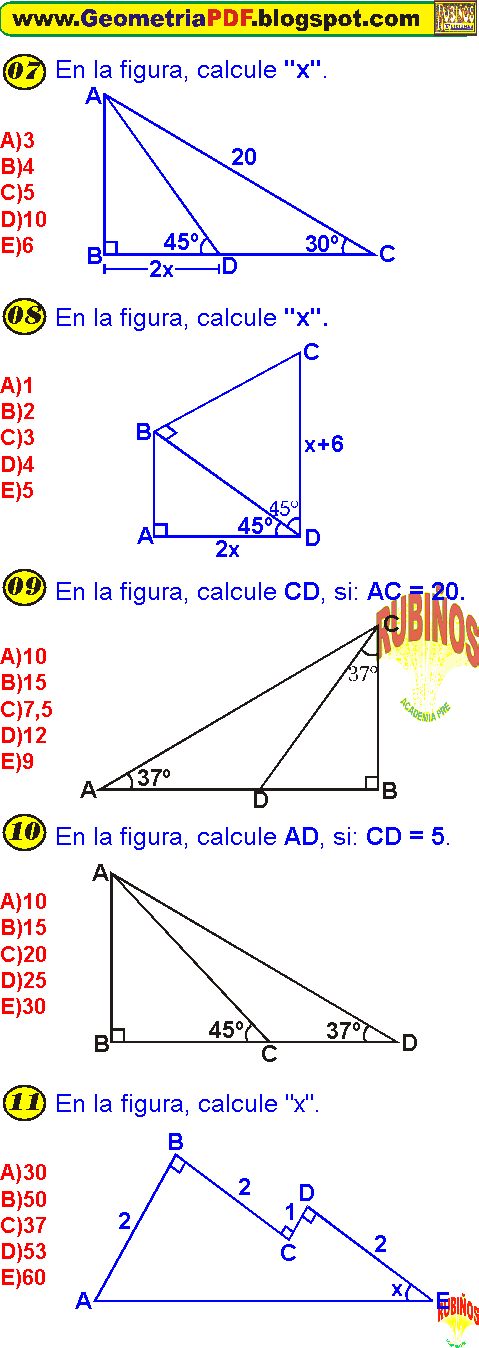
TRIÁNGULOS NOTABLES PROBLEMAS RESUELTOS PDF

Demostración del Triangulo de 30° y 60°: Considerando un triángulo equilátero cuyo lado mide “2a”, se traza la altura que también es mediana y bisectriz, entonces por Pitágoras : En el BHC (30° y 60°) el cateto adyacente a 60° mide la mitad de la hipotenusa. TEOREMA : Si un cateto mide la mitad de la hipotenusa, entonces el ángulo agudo adyacente a dicho cateto mide 60°. Demostración del Triangulo de 45° y 45°: Considerando un cuadrado cuyo lado mide “a”, se traza la diagonal formándose ángulos de 45° entonces, por Pitágoras TRIÁNGULOs RECTÁNGULOs NOTABLEs DE MEDIDA APROXIMADA : • El cateto que se opone a 37° tiene una longitud igual a 3K. • El cateto que se opone a 53° tiene una longitud igual a 4K. • La hipotenusa tiene una longitud igual a 5K. • “K” es un valor constante. TRIÁNGULOS RECTÁNGULOS NOTABLES Denominamos así a aquellos triángulos rectángulos en los cuales conociendo las medidas de sus ángulos internos (denominados ángulos notables) se establece una determinada relación entre las longitudes de sus lados y viceversa. TRIÁNGULOS RECTÁNGULOS NOTABLES DE MEDIDAS EXACTAS Triángulo Rectángulo Notable: (20°–70°) Triángulo Rectángulo Notable: (40°–50°) Triángulo Rectángulo Notable: (18°30’–71°30’) Triángulo Rectángulo Notable: (26°30’–63°30’) Triángulo Rectángulo Notable: (15°–75°) Triángulo Rectángulo Notable: (22°30’–67°30’) Triángulo Rectángulo Notable: (36°–54°) Triángulo Rectángulo Notable: (18°–72°) EJEMPLOS : Triángulo Rectángulo Notable: (14°–76°) : Triángulo Rectángulo Notable: (16°–74°) : Triángulo Rectángulo Notable: (8°–82°)