GEOMETRÍA SAN MARCOS A-B-D DECO SOLUCIONES DEL EXAMEN ADMISIÓN UNIVERSIDAD PRUEBA RESUELTA PREGUNTAS DESARROLLADAS PDF

PREGUNTA 1 :

Pedro dispone de una hoja de papel de forma triangular. Ha dividido en tres partes iguales cada uno de los lados de la hoja, trazando segmentos. Luego, ha sombreado una región triangular y una región cuadrangular de la hoja, tal como se muestra en la figura. Si el área de la región triangular sombreada es 10 cm², ¿cuál es el área de la región cuadrangular sombreada?

A) 30 cm²

B) 50 cm²

C) 70 cm²

D) 40 cm²

RESOLUCIÓN :

Rpta. : "B"

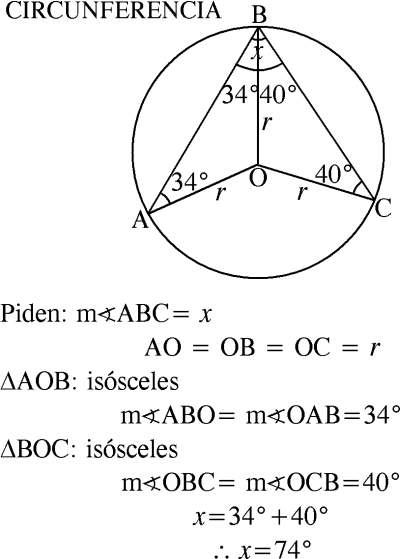
PREGUNTA 2 :

En la clase de Geometría, el profesor indica la importancia de la circunferencia en diferentes aspectos de la vida diaria; para ello utiliza un transportador que, como sabemos, nos sirve para medir ángulos o dibujar circunferencias, tal como se muestra en la figura. Si el punto O es centro de la circunferencia, ¿cuál es la medida del ángulo ∠ABC?

A) 68º

B) 72º

C) 84º

D) 74º

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 3 :

Carla debe colocar clavos sobre los puntos A, B, C y D, sobre una mesa, y tender una cuerda que una estos puntos de forma tal que ABC sea un triángulo y se cumpla la relación de los ángulos, como se muestra en la figura. Si la longitud de AB es 8 cm, ¿cuáI es la longitud mínima entera de BD?

A) 6 cm

B) 7 cm

C) 4 cm

D) 5 cm

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 4 :

En la figura se representa un pozo de agua que tiene forma parabólica, donde A(8;y), B(12; 0), C( – 12;0) y el vértice de la parábola V(0;– 18). Halle el valor de y.

A) – 8

B) – 12

C) – 9

D) – 10

RESOLUCIÓN :

Rpta. : "D"

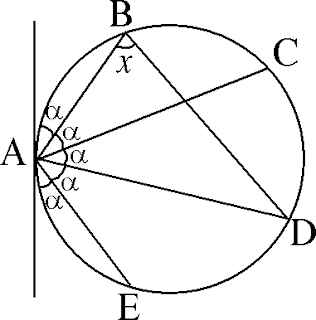
PREGUNTA 5 :

Mario dibuja cinco puntos, A, B, C, D y E, en una circunferencia, así como la recta tangente a la circunferencia en A, como se muestra en la figura, de tal manera que los cinco ángulos marcados con a son congruentes. Halle el valor de x.

A) 36°

B) 45°

C) 53°

D) 72°

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 6 :

A) 3√3/4 cm

B) √3 cm

C) 3√3/5 cm

D) 3√3/2 cm

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 7 :

En la figura, AB=AD, m∠BAC= 50º, m∠BCA= 30º y m∠CAD=10º.
Halle la medida del ángulo ∠ACD.
A) 12º
B) 9º
C) 10º
D) 15º
RESOLUCIÓN :
Rpta. : "C"

PREGUNTA 8 :

En un triángulo rectángulo ABC, recto en B, se traza la mediana BM (M en AC). Luego, sobre BC y MC, se ubican, respectivamente, los puntos P y Q, tal que PQ=QC. Si MQ= 6 cm, halle la distancia entre los puntos medios de los segmentos MP y BQ.

A) 4 cm

B) 2√3 cm

C) 3 cm

D) 3√2 cm

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 9 :

En la figura, el punto P, situado al borde de la ventana rectangular ACDE, dista 30 cm del segmento AB. Si BP es bisectriz del ángulo ∠ABD y PA es bisectriz del ángulo ∠BAE, calcule DE.

A) 60 cm

B) 90 cm

C) 45 cm

D) 30 cm

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 10 :

A) 74°

B) 75°

C) 76°

D) 78°

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 11 :

La figura representa un parque de forma elíptica. Colocamos su centro en el origen de coordenadas y su eje mayor contenido en el eje X. Si se sabe que el borde elíptico pasa por los puntos P (10√6; −10) y Q(20; 10√2) , halle su ecuación.

A) [x²/800 ] + [y²/400 ] =1

B) [x²/800 ] + [y²] =1

C) [x²/400 ] + [y²/200 ] =1

D) [x²/300 ] + [y²/900 ] =1

RESOLUCIÓN :

Rpta. : "A"

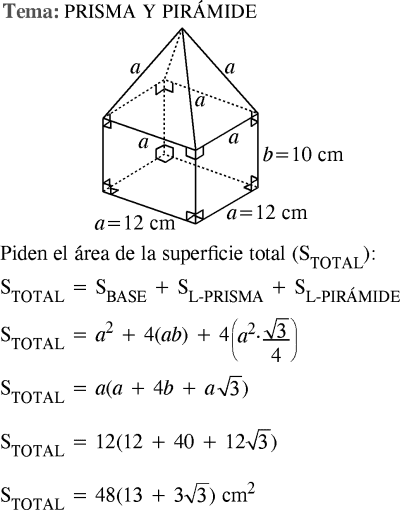
PREGUNTA 12 :

En una empresa se realizó un intercambio de regalos para fomentar el compañerismo entre sus trabajadores. Uno de esos regalos se representa en la figura, cuya base es un prisma cuadrangular regular, y la parte superior es una pirámide cuadrangular regular con caras laterales en forma de triángulos equiláteros. Calcule el área de la superficie de dicho regalo.

A) 42(15 + 3√3) cm²

B) 144(3 + √3) cm²

C) 24(11 + 3√3) cm²

D) 48(13 + 3√3) cm²

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 13 :

En la figura 1, se tiene una esfera de madera compacta de 5 cm de radio. Para colocarla sobre la mesa y para que no ruede, se le va a seccionar con un plano a una distancia de 4 cm del centro, desechando la menor cantidad de madera. Halle el volumen del sólido que queda sobre la mesa, considerando que la sección de corte está sobre la mesa. Ver figura 2.

A) 165𝛑 cm³

B) 162𝛑 cm³

C) 166𝛑 cm³

D) 168𝛑 cm³

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 14 :

Un balde, que tiene la forma de un tronco de cono circular recto, contiene agua hasta la mitad de su altura, como se muestra en la figura. Se sumerge por completo un trozo de metal dentro del balde y el nivel del agua en el balde sube 15 cm. Si la altura del balde es 60 cm y los radios de sus bases miden 10 cm y 18 cm, ¿cuál es el volumen del trozo de metal?

A) 3290𝛑cm³

B) 3370𝛑cm³

C) 3280𝛑cm³

D) 3380𝛑cm³

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 15 :

Las rectas 3y–x–6= 0, x = 0, y = 0 determinan una región triangular. Al hacer girar esta región alrededor del eje x se genera un sólido de revolución. Calcule el volumen de dicho sólido.

A) 24𝛑u³

B) 6𝛑u³

C) 8𝛑u³

D) 18𝛑u³

RESOLUCIÓN :