LA CIRCUNFERENCIA Y SUS PROPIEDADES EJERCICIOS RESUELTOS DE GEOMETRÍA PREUNIVERSITARIA PDF
Si una circunferencia se divide en varios arcos, la suma de las medidas de todos estos arcos es 360°.
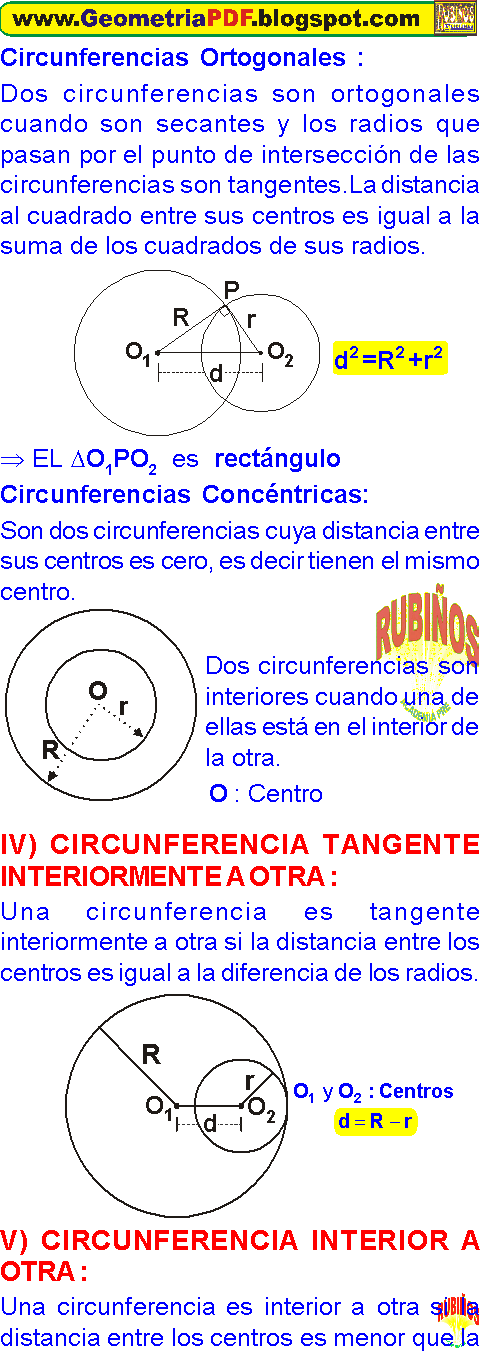
* Cuando dos circunferencias son tangentes exteriores o interiores, la recta que pasa por los centros también pasa por el punto de tangencia.
* Circunferencia inscrita en un triángulo es la circunferencia que es tangente a los tres lados. Al radio de esta circunferencia también se le llama inradio.
* Un cuadrilátero es circunscrito a una circunferencia cuando sus cuatro lados son tangentes a dicha circunferencia.
* Un cuadrilátero es exinscrito a una circunferencia, cuando las prolongaciones de sus cuatro lados son tangentes a una misma circunferencia.
* Un cuadrilátero es inscrito en una circunferencia cuando sus vértices se encuentran sobre la circunferencia.
Un cuadrilátero es inscriptible en una circunferencia cuando se puede inscribir en una circunferencia.
En el gráfico se muestra a una circunferencia inscrita al triángulo y a la vez el triángulo está circunscrito a la circunferencia. I : Incentro del triángulo ABC. r : Inradio del triángulo ABC. La mediana de un trapecio rectángulo circunscrito a una circunferencia mide 18 cm y uno de los ángulos, 53°. Calcular el radio de la circunferencia inscrita A)2 cm B)8 cm C)6 cm D)3 cm E)5 cm Si: ABCD es un trapecio isósceles, AB = 3. Hallar el perímetro de dicho trapecio A)3 B)6 C)9 D)12 E)15 Calcular el semiperímetro de un triángulo rectángulo, sabiendo que el inradio mide 2m y la longitud de la hipotenusa es 13 m. A)12 m B)13 m C)15 m D)21 m E)28 m Los catetos de un triángulo miden . Calcular la medida de su inradio. a) 1 b) 2 c)3 d) 4 e) 5 En la figura, calcule x a) 30° b) 53° c) 37° d) 45° e) 60° Un triángulo ABC recto en B esta inscrito en una circunferencia. Calcular la longitud del radio de la circunferencia circunscrita al triángulo ABC en función de las longitudes de los radios r1 y r2 de las circunferencias máximas inscritas a los segmentos circulares determinados por los catetos , y de la longitud r del radio de la circunferencia inscrita al triángulo ABC. A) r + r1 + r2 B) 2 (r + r1 + r 2) C) r + 2 (r1 + r2) Sea el cuadrilátero ABCD convexo , , sea O1 el centro de la circunferencia inscrita en el cuadrilátero AMND, O2 el centro de la circunferencia inscrita en el cuadrilátero NMBC. Si AB + CD = 40m, AD + BC = 24 m. Halle MN A)8m B)9m C)10m D) 11m E)12m De la figura r = 3cm , AB =7cm., CD =7,5 cm. y AD = 4 cm. Calcular BC: A)10,6 cm B)10,5 C)10,3 D)10,7 E)11 Se tiene un triángulo rectángulo ABC recto en B, en el cual las bisectrices de los ángulos internos de A y C cortan a los catetos en E y F respectivamente. Si la proyección de sobre la hipotenusa mide 5,4u. Halle la medida del radio del triángulo ABC (en u). A)2,0 B) 2,5 C) 2,7 D) 2,75 E) 2,8 En un cuadrilátero ABCD, circunscrito a una circunferencia si ; AD + BC = 15u, CD = 9u. Calcular la medida del radio de la circunferencia (en u). TEOREMAS RELACIONADOS A LA CIRCUNFERENCIA 1. Circunferencia Inscrita Se dice que una circunferencia está inscrita en un polígono, si se encuentra en el interior de éste y sus lados son tangentes a dicha circunferencia. A su radio se le llama INRADIO. • r : INRADIO • ABC : Triángulo circunscrito • ABCD : Cuadrilátero circunscrito • La circunferencia es inscrita 2. Circunferencia Circunscrita Es aquella circunferencia que pasa por todos los vértices de un polígono. A su radio se le llama CIRCUNRADIO. • R : Circunradio • O : Circuncentro • ABC : Triángulo inscrito • ABCD : Cuadrilátero inscrito • La circunferencia es circunscrita. 3. Circunferencia Exinscrita Se dice que una circunferencia es exinscrita a un triángulo, si se encuentra en el exterior de dicho triángulo y es tangente a un lado y a las prolongaciones de los otros dos lados. A su radio se le llama EXRADIO. F, T y E: Son puntos de tangencia. • ra : Exradio Relativo al lado BC • ABC : Triángulo exinscrito • En todo triángulo, hay tres circunferencias exinscritas. TEOREMAS DE TANGENTE 1. Las tangentes trazadas desde un punto exterior a una circunferencia son congruentes. PA = PB Demostración: OAP OBP (4º caso) PA = PB l.q.q.d. 2. Los tangentes interiores comunes a dos circunferencias exteriores son congruentes y la recta que pasa por los centros también pasa por el punto de intersección de dichas tangentes. AB = CD Demostración 1) PA = PD 2) PB = PC Sumando: PA+PB=PD + PC AB = CD l.q.q.d. 3. Los tangentes exteriores comunes a dos circunferencias son congruentes y su punto de intersección se halla sobre la recta que pasa por los centros. AB = CD Demostración 1) PA = PD 2) PB = PC Restando PA – PB = PD – PC AB = CD lqqd. TEOREMA DE PITOT En todo cuadrilátero circunscrito a una circunferencia o circunscriptible, se cumple que la suma de las medidas de dos lados opuestos es igual a la suma de las medidas de los otros dos lados. AB + CD = BC + AD Demostración AB = x + n CD = y + m Sumando: AB + CD = x + y + n + m AB + CD = BC + AD lqqd GENERALIZANDO: En todo polígono circunscrito con un número par de lados, la suma de los lados no consecutivos es igual a la suma del resto de lados. TEOREMA DE STEINER En todo cuadrilátero exinscrito o exinscriptible la diferencia de las medidas de dos lados opuestos es igual a la diferencia de las medidas de los otros dos lados. AB – CD = AD – BC Demostración 1) AM = AN AB + BP = AD + DR AB + BC + x = AD + CD + x AB – CD = AD – BC l.q.q.d. TEOREMA DE PONCELET En todo triángulo rectángulo la suma de las medidas de los catetos es igual a la medida de la hipotenusa mas la medida del diámetro de la circunferencia inscrita. AB + BC = AC + 2r r : Inradio Demostración AB = m + r BC = n + r Sumando: AB + BC = m + n + 2 r l.q.q.d. AB + BC = AC + 2r PROPIEDADES 1. En todo triángulo circunscrito se cumple: x = p – AC y = p – BC z = p - AB Demostración 1) 2x + 2y + 2z = perímetro (ABC) 2) mitad x + y + z = p x + AC = p x = p – AC lqqd 2. En todo triángulo ex-inscrito se cumple: AP = AQ = p p : Semiperímetro del ABC Demostración Perímetro (ABC) = AB + BC + AC = AB + x + y + AC = AP + AP Perímetro (ABC) = 2AP Mitad p = AP lqqd 3. Circunferencias exinscritas relativas al lado AB y al lado BC, cumple: FA = CE Demostración 1) FA + AC = semiperímetro (ABC) 2) AC + CE = semiperímetro (ABC) 3) Igualando FA + AC + AC + CE FA = CE lqqd 4. Circunferencia exinscrita relativa al lado AB y circunferencia inscrita, cumple: x = y PA = AF = x BE =BG = y Demostración PC = DC x + x + a + b = a + y + y + b 2x = 2y Mitad x = y L.q.q.d. 5. La suma de las medidas de los radios de las circunferencias exinscritas relativas a los catetos de un triángulo rectángulo, es igual a la medida de la hipotenusa. Recomendaciones para resolver problemas de ángulos en la circunferencia 1. Se tiene dos circunferencias tangentes interiormente o tangentes exteriormente, por lo general los datos están en una circunferencia y la incógnita está en la otra, trace en estos casos por el punto de contacto una tangente común. TANGENTE COMÚN 2. Debemos tener en cuenta que la medida del ángulo semi-inscrito es igual a la medida del ángulo inscrito que subtiende el mismo arco. mACB = mABD 3. Debemos tener en cuenta que la medida del ángulo adyacente a un ángulo circunscrito es igual a la medida del arco que subtiende los lados de este último. = mAC Demostración : ángulo circunscrito + = 180º mAC + = 180º Igualando: = mAC lqqd CUADRILÁTERO INSCRITO Es aquel cuadrilátero que tienen sus cuatro vértices en una misma circunferencia. CASO I CASO II CASO III + = 180º = = CUADRILÁTERO INSCRIPTIBLE Es aquel cuadrilátero que puede inscribirse en una circunferencia, para ello debe cumplir cualquiera de los casos de cuadrilátero inscrito o de la propiedad, sin que se dibuje la circunferencia. Ejemplo: El rectángulo, el cuadrado, el trapecio isósceles. AB BC RECTAS ANTIPARALELAS Dos rectas son antiparalelas con respecto a los lados de un ángulo, cuando forman con los lados del ángulo, un cuadrilátero inscriptible. ABCD: Cuadrilátero inscriptible EJERCICIOS RESUELTOS 1. Sobre la hipotenusa AC de un triángulo rectángulo ABC se construye exteriormente el cuadrado ACEF de centro O. Calcular la medida del ángulo OBC. a) 30º b) 36º c) 45º d) 53º e) 60º Resolución El cuadrilátero ABCO es inscriptible ya que: mABC + mAOC = 180º