CUADRILÁTEROS EJEMPLOS Y PROBLEMAS RESUELTOS PDF
Los objetivos de estudio serán :
• Conocer las definiciones y teoremas de cada clase de cuadrilátero.
• Aprender las propiedades de los trapecios y paralelogramos.
• Plantear y resolver problemas al emplear la teoría de cuadriláteros.
¿POR QUÉ ES NECESARIO ESTE CONOCIMIENTO?
Porque nos proporcionará conocimientos de apoyo para comprender de manera sencilla los temas a desarrollar.
Además nos ayudará a planificar de manera adecuada la disposición de las medidas de terrenos de cultivo; avenidas, calles y jirones; asimismo de edificios y otras construcciones.
► Edificio moderno que tiene partes en forma de paralelogramos y trapecios
► Construcción incaica en donde se pueden ver formas trapeciales
► Cristales de pirita, se puede apreciar formas cuadradas
CLASIFICACIÓN DE CUADRILÁTEROS ( según sus lados opuestos paralelos)
► Trapezoides
► Trapecios
► Paralelogramos
En un paralelogramo ABCD, se traza bisectriz del ángulo ABC (“M” en ) siendo : AM = MD; BC = 10u y BM = 6u. Calcular la distancia de “C” al lado . A)6u B)5 C) 4,2 D) 5,4 E) 4,8 Hallar “x”, si: A) 32° B) 24° C) 36° D) 42° E) 54° Los lados de un trapecio ABCD son iguales. Si es paralelo a y tiene el doble de la longitud de ; la diagonal : A) es perpendicular a la diagonal . B) Es la bisectriz del ángulo A. C) Tiene por longitud el promedio de las longitudes de . D) Tiene como longitud el promedio de las longitudes de . E) Divide en partes iguales a la diagonal. En el trapecio ABCD mostrando , los ángulos miden 144° y 72° respectivamente. Si la diferencia de las bases es 24. Hallar CD. A) 30 B) 18 C) 24 D) 12 E) 6 En un trapecio ABCD, de bases , se trazan las bisectrices de los ángulos A y D que se cortan en R y las bisectrices de los ángulos B y C que se cortan en S. Hallar RS, si AB = 4, CD=12, AD=7 y BC = 9. En la figura , los lados son paralelos. Si : AB = 5 y BC = 12. Hallar la longitud del segmento A) 17 B) 12 C) 20 D) 10 E) 18 Si ABCD es un trapecio isósceles y CDE un triángulo isósceles , hallar x. A) 45° B) 50° C) 60° D) 55° E) 47° En un trapecio de ABCD: hallar: A) 20° B) 30° C) 40° D) 45° E) 60° Calcular la mediana del trapecio ABCD, si : BC = 4u. A) 3u B) 4 C) 5 D) 6 E) 7 Si ABCD es un romboide, tal que: AD=14u y CD=8u. Hallar la longitud del segmento que une los puntos medios de AB y ED. A) 8u B) 10 C) 12 D) 14 E) 9 Si: CD = 10u, hallar la longitud del segmento que une los puntos medios de . A) 4u B) 3 C) 3,5 D) 5 E) 6
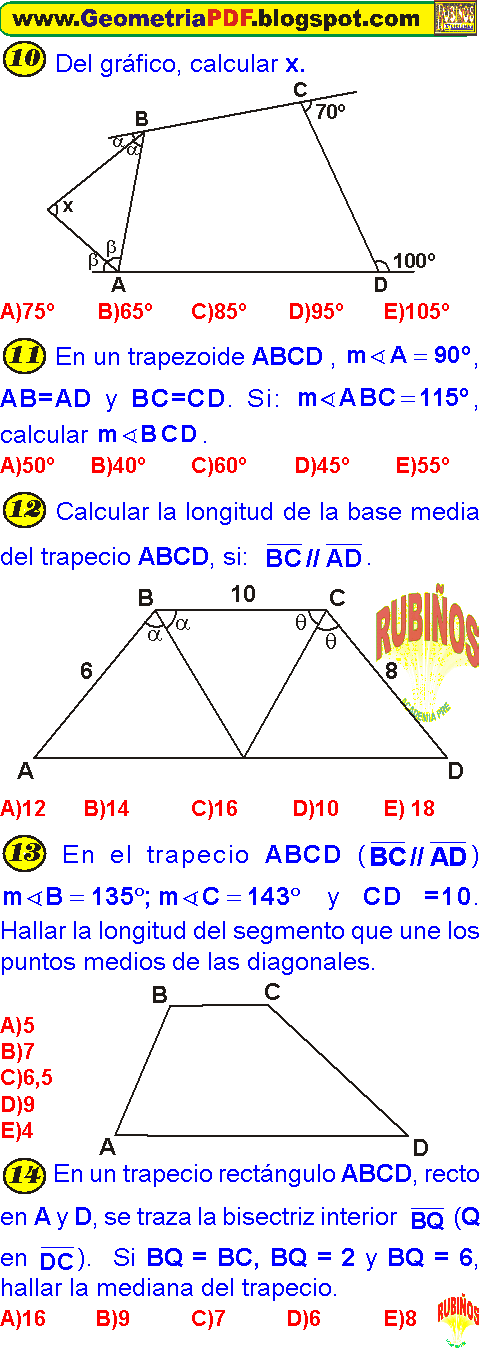
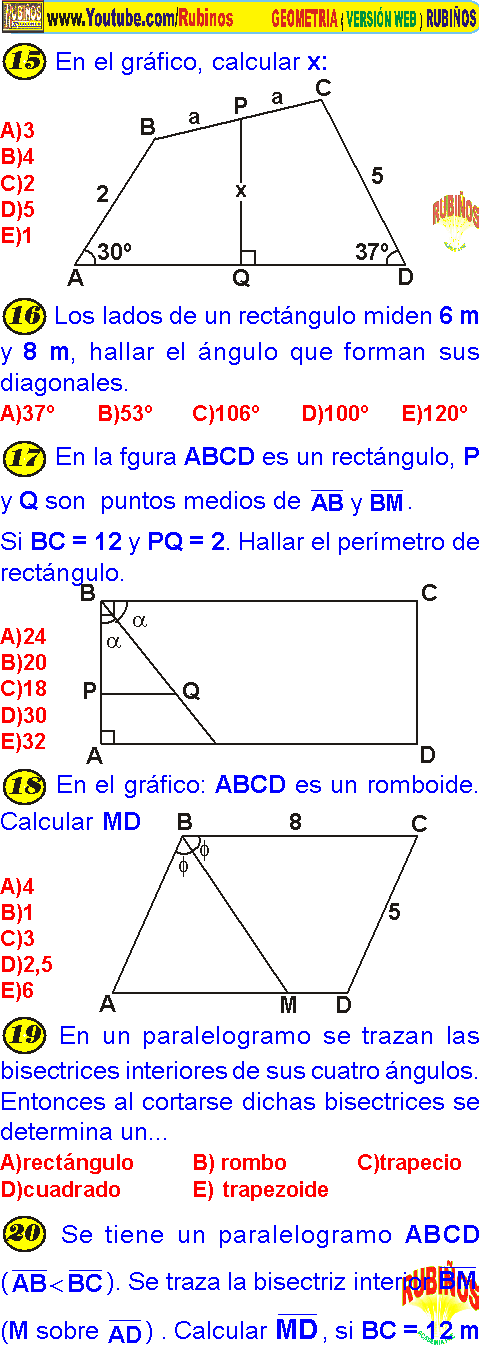
En el trapecio ABCD, calcular x, si: . A)10º B)12º C)15º D)18º E) 16º En el trapecio isósceles ABCD, calcular x, si: . En el gráfico, calcular x, si: a+b=200°. A)110º B)76º C)90º D)85º E)100º Calcular x, si: . A)8 B)6 C)10 D)12 E) 15 Las longitudes de las bases y de la base media de un trapecio suman 60. Calcular la longitud de la base media. A)40 B)45 C)15 D)30 E) 20 Calcular el perímetro del trapezoide simétrico ABCD. Del gráfico, calcular x. A)75º B)65º C)85º D)95º E)105º En un trapezoide ABCD , , AB=AD y BC=CD. Si: , calcular . A)50º B)40º C)60º D)45º E)55º Calcular la longitud de la base media del trapecio ABCD, si: . A)12 B)14 C)16 D)10 E) 18 En el trapecio ABCD () y CD =10. Hallar la longitud del segmento que une los puntos medios de las diagonales. A)5 B)7 C)6,5 D)9 E)4 En un trapecio rectángulo ABCD, recto en A y D, se traza la bisectriz interior (Q en ). Si BQ = BC, BQ = 2 y BQ = 6, hallar la mediana del trapecio. A)16 B)9 C)7 D)6 E)8 PROBLEMA 14 : Si: CD = 10u, hallar la longitud del segmento que une los puntos medios de . A) 4u B) 3 C) 3,5 D) 5 E) 6 RESOLUCIÓN: Se prolonga y se traza CHD (D de 37° y 53°): ABHD : AD = BH = 8 + a ABCD : RPTA : ‘‘A’’ PROBLEMA 15 : Si : AC = 24u , calcular la longitud del segmento que une los puntos medios de . A) 6u B) 5 C) 4 D) 3 E) 8 RESOLUCIÓN: Como: AC=24u AMNC: RPTA : ‘‘A’’ PROBLEMA 16 : En un paralelogramo ABCD, se traza bisectriz del ángulo ABC (“M” en ) siendo : AM = MD; BC = 10u y BM = 6u. Calcular la distancia de “C” al lado . A)6u B)5 C) 4,2 D) 5,4 E) 4,8 RESOLUCIÓN : ABCD : Como : DABM (Isósceles): AB = AM = 5u Se traza: ABF : (de 53° y 37°) Se traza : MBN ( de 53° y 37°) RPTA : ‘‘E’’ PROBLEMA 6 : En el trapecio, calcular “x”. A) 8 B) 15/2 C) 31/4 D) 6 E) 10 RESOLUCIÓN: Por la propiedad de la mediana , se obtendrá RPTA : ‘‘c’’ PROBLEMA 7 : En la figura: , calcular A) 30° y 20° B) 60° y 50° C) 60° y 98° D) 60° y 110° E) 70° y 105° RESOLUCIÓN: De la figura: (ángulo consecutivo en un trapecio). Ahora (ángulos consecutivos en un trapecio). RPTA : ‘‘d’’ PROBLEMA 8 : Si ABCD es un paralelogramo, calcular “AC”. A) 16 B) 8 C) 10 D) 12 E) 9 RESOLUCIÓN : Las diagonales BD y AC se bisecan: Entonces el AOH es notable (30° y 60°) Luego: AC = 8 RPTA : ‘‘b’’ PROBLEMA 9 : En el trapecio ABCD , hallar “PQ”, si : AP = PC A) 4 B) 5 C) 10 D) 3 E) 2 RESOLUCIÓN: Como “P” es punto medio y es punto medio. Por propiedad de los puntos medios de las diagonales: RPTA : ‘‘d’’ PROBLEMA 10 : En un trapecio de ABCD: hallar: A) 20° B) 30° C) 40° D) 45° E) 60° RESOLUCIÓN : Por datos los ángulos “A”, “B”, “C” y “D” son proporcionales a 3 ; 5 ; 6 y 2. Entonces :