GEOMETRÍA UNI EXAMEN RESUELTO DE ADMISIÓN A LA UNIVERSIDAD DE INGENIERÍA

Sabiendo que L1//L2 y θ es la medida de un ángulo agudo. Calcule el mínimo valor entero de “x”.

A) 41°

B) 42°

C) 44

D) 45°

E) 46°

22.

En un triángulo ABC, mËBAC = 2(mËACB) = 30°, si se traza la mediana BM, calcule mËABM. A) 75° B) 80° C) 90° D) 100° E) 105°

23.

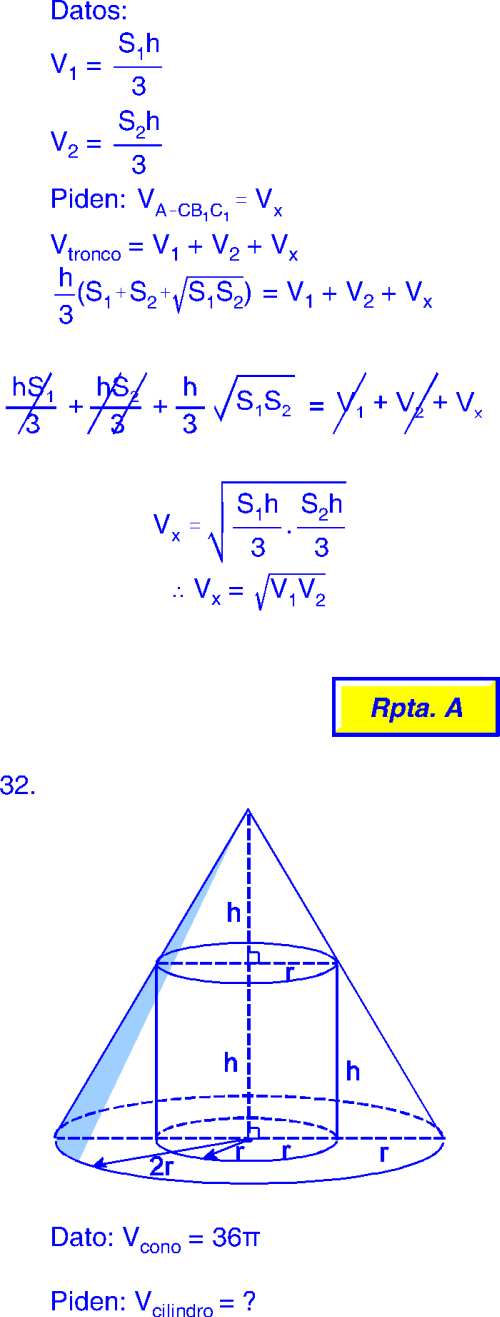
El cateto AB del triángulo rectángulo ABC se divide en 8 partes congruentes. Por los puntos de división se trazan 7 segmentos paralelos al cateto AC tal como se muestra en la figura. Si AC = 10 m, halle la suma (en m) de las longitudes de los 7 segmentos. A) 33 B) 34 C) 35 D) 36 E) 37 24. En un cuadrilátero ABCD, las diagonales miden AC = 17 cm y BD = 15 cm; sea "M" punto medio de AC y "F" punto medio de BD; los ángulos interiores de B y D miden 90°. Calcule MF en cm. A) 2 B) 3 C) 4 D) 5 E) 6 25. Al cortarse dos cuerdas de una misma circunferencia perpendicularmente, una de ellas queda dividida en segmentos de 3 y 4 unidades y la otra en segmentos de 6 y 2 unidades. Determine el diámetro de la circunferencia. A) 87 B) 73 C) 68 D) 65 E) 63 26 L a f i g u r a mu e s t r a t r e s semicircunferencias y la longitud de la circunferencia mayor es 10π u. Si AB= 24 u, siendo AB tangente a las semicircunferencias interiores, calcule la longitud (en u) de la circunferencia menor. A) 2π B) 3π C) 4π D) 5π E) 6π 27. Para tres circunferencias tangentes (exteriormente) dos a dos, la suma de sus radios es 10 cm y el producto de los mismos es 40 cm3. Halle el área (en cm2) de la región triangular cuyos vértices son los centros de la circunferencia. A) 18 B) 18,5 C) 19 D) 19,5 E) 20 28. El punto A está a 8 m encima de un plano horizontal P, y el punto B se halla a 4 m encima del mismo plano. Si C es un punto del plano P tal que AC + BC es mínimo y el ángulo que forman la recta CB con el plano P es wv 53°, entonces (en m) AC es: A) 8 B) 8,5 C) 9 D) 9,5 E) 10 29. Las caras de un triedro equilátero de vértice V miden 60°. En una de sus aristas se considera un punto R de tal manera que VR = 2 cm. Por R pasa un plano perpendicular a VR, que interseca a las otras aristas en S y T. Halle el área del triángulo RST (en cm2). A) 3 2 B) 2 6 C) 26 D) 3 3 E) 4 2 30. Sea el tetraedro regular de arista a, con a un entero positivo diferente de múltiplo de 3. Se unen los baricentros de las caras del tetraedro regular formando un tetraedro nuevo y así se repite el proceso n veces. Si , donde Sn y Vn son el área Sn Vn ' 243 6 4 total y el volumen del tetraedro respectivamente en el proceso n-ésimo. Halle 81 6 hn, siendo hn la altura del tetraedro en el proceso n-ésimo. A) 8 3 B) 16 C) 8 6 D) 16 2 E) 32 31. En un tronco de pirámide ABC - A1B1C1 los volúmenes de las pirámides B1 - ABC y A - A1B1C1 miden V1 y V2 respectivamente. Determine el volumen de la pirámide A - CB1C1. A) V B) C) 1V2 V1V2 V1 %V2 2V1V2 V1 %V2 D) 2 V E) 3 1V2 V1V2 6 32. El volumen de un cono de revolución es 36π cm3. Se inscribe un triángulo equilátero ABC en la base del cono. El triángulo ABC está circunscrito a una circunferencia cuyo círculo es base de un cilindro recto inscrito en el cono. Calcule el volumen del cilindro (en cm3). A) 27π B) C) 10 27π 8 27π 5 D) E) 27π

GEOMETRÍA UNI EXAMEN RESUELTO DE ADMISIÓN A LA UNIVERSIDAD DE INGENIERÍA

Prueba Resuelta