GEOMETRÍA PUCP EXAMEN INGRESO UNIVERSIDAD CATÓLICA PRUEBA DE ADMISIÓN SOLUCIONARIO PRIMERA OPCIÓN EVALUACIÓN DE TALENTO DESARROLLADA PDF
PREGUNTA 21 :
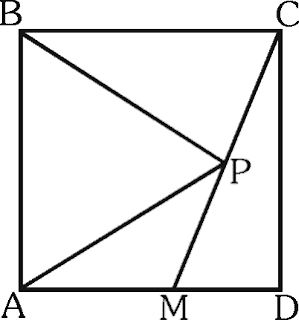
Sea ABCD un cuadrado y el triángulo ABP es equilátero, calcula m∠CMD.
A) 15°
B) 45°
C) 60°
D) 75°
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 22 :
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 23 :
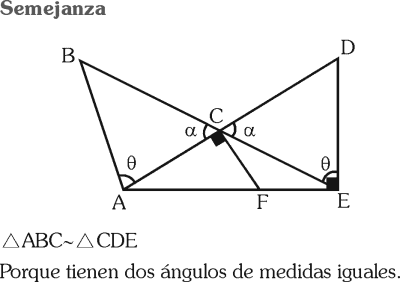
En un triángulo acutángulo ABC se trazan las alturas AN y CM, tal que AM=2 u, MB=3 u y BC=6 u. Calcula BN.
A) 2,25 u
B) 2,5 u
C) 2,75 u
D) 3,5 u
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 24 :
Si la longitud de una circunferencia es igual al perímetro de un cuadrado, el área que limita la región de la circunferencia es A y el área del cuadrado es B. Calcula B/A
A) 4/𝛑
B) 2/𝛑
C) 𝛑/2
D) 𝛑/4
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 25 :
Se tiene un sector circular cuyo ángulo central es 2𝛑/5 rad . Calcula la relación de áreas de dicho sector y el círculo al cual pertenece.
A) 2/5
B) 1/4
C) 1/6
D) 1/5
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 26 :
En una pirámide cuadrangular regular el apotema de la base es 6 cm y el apotema del sólido es 10 cm. Calcula el volumen de la pirámide.
A) 250 cm³
B) 384 cm³
C) 275√3 cm³
D) 420 cm³
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 27 :
En un prisma hexagonal regular ABCDEF-GHIJKL, se inscribe una pirámide regular tal que su base coincide con la base ABCDEF y su vértice coincide con el centro de la base superior. La arista lateral de la pirámide mide 20 u y forma con el plano de la base un ángulo cuya medida es 60º. Calcule el volumen del Prisma.
A) 3 500 u³
B) 4 200 u³
C) 4 500 u³
D) 5 200 u³
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 28 :
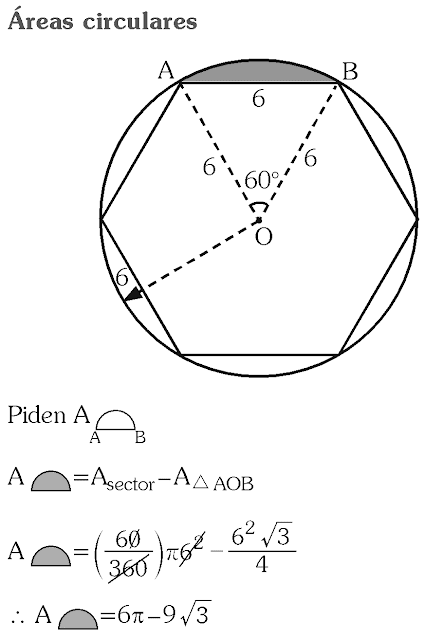
En un hexágono regular inscrito en una circunferencia de radio 6 u, calcula el área de uno de los segmentos circulares determinados por un lado del hexágono regular y la circunferencia.
A) 7π – 6√3
B) 6π – 9√3
C) 8π – 9√3
D) 9π – 6√3
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 29 :
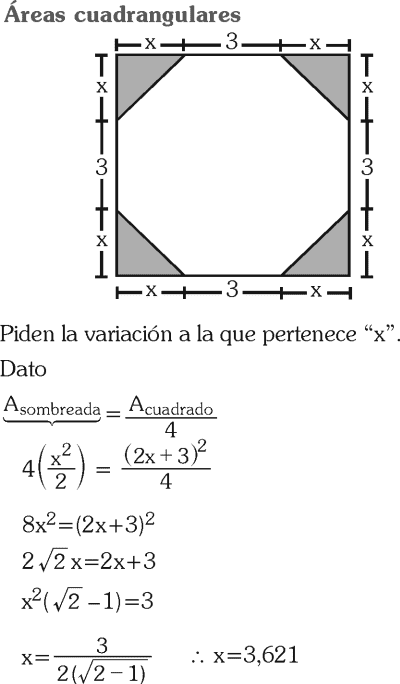
En el gráfico, la suma de las áreas de las regiones sombreadas isósceles es igual a la cuarta parte del área de la región cuadrada ABCD; encuentra a qué intervalo pertenece “x”.
A) 0,5 < x < 1
B) 1 < x < 2,5
C) 2,5 < x < 3,1
D) 3,1 < x < 4
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 30 :
En la pirámide P–ABC, de altura PA , M es punto medio de PC y AM=BC. Si m∠ABC=90°, calcula el orden de las medidas de los ángulos CPB , PCB y PBC.
A) 45°, 45°, 90°
B) 30°, 75°, 75°
C) 30°, 60°, 90°
D) 60°, 60°, 60°
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 31 :
En una semicircunferencia de diámetro AB=12 cm se inscribe el triángulo ACB, por el centro de la semicircunferencia se traza una paralela de AC interceptando a BC en Q y en P a la tangente trazada a la circunferencia en B. Si BC=8, calcula PB.
A) 2√2
B) 3√2
C) 5√2
D) 10
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 32 :
Un cono circular recto invertido se llena de agua hasta la mitad su altura, de 10 cm y radio en la base 4 cm. Si se introduce un cilindro de altura 1 cm y radio en su base 2 cm, calcula la altura del desnivel del agua sufrido en el cono invertido.
a) 3∛133 – 4,5
b) 3∛133 – 5
c) 3∛133 – 4
d) 3∛133 – 3
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 33 :
Si el volumen de un cilindro recto es el doble del volumen de un cono recto, tal que los radios de sus respectivas bases tienen igual medida; calcula la relación entre las alturas del cilindro y cono, respectivamente.
a) 1/4
b) 2/3
c) 3/4
d) 1
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 34 :
Del gráfico mostrado, el triángulo AMD es equilátero y CD=8 u. Sean A₁ y A₂ las regiones sombreadas, calcula A₁×A₂.
A) 64 u²
B) 108/3 u²
C) 128/3 u²
D) 149/3 u²
RESOLUCIÓN :
Rpta. : "C"