1RO 2DO ACTIVIDAD 7 EXPERIENCIA 9 MATEMÁTICA APRENDO EN CASA PRIMERO SEGUNDO DE SECUNDARIA TAREA WEB RETO TV RADIO APRENDIZAJE 2021 PDF
Actividad 7–1°–2° grado
EXPERIENCIA DE APRENDIZAJE INTEGRADA 9
DISEÑAMOS UNA ESTRUCTURA COMPUESTA DE UN PRISMA Y UNA PIRÁMIDE QUE SOLUCIONE UN ASUNTO PÚBLICO
En esta actividad realizaremos el boceto de la estructura de una edificación, que busca dar solución a un asunto público.
Recordemos grabar un video o tomar fotografías de las tareas realizadas.
Luego, los aplicativos Quik y Snapseed para editar las evidencias de las actividades que realizaremos.
NOS PREPARAMOS PARA REPRESENTAR FIGURAS Y CUERPOS GEOMÉTRICOS
Es importante apoyarnos con la familia, por ello le podemos consultar sobre las dimensiones que podría tener la edificación que nos proponemos diseñar.
Ahora respondemos las siguientes preguntas en el cuaderno:
¿A qué situación problemática podemos dar solución con tu diseño?
¿Qué dimensiones tiene el terreno donde te propones realizar la construcción?
¿Qué tipo de prisma emplearás para el cuerpo de la estructura de la edificación?
¿Qué altura tendrán las paredes?
¿Qué beneficio nos brinda los techos con forma piramidal?
¿Qué tipo de pirámide para el techo de la edificación?
¿Qué altura tendrá el techo?
GRAFICAMOS A PARTIR DE MODELOS DADOS
Antes de iniciar a bosquejar debemos tener los instrumentos de dibujo.
Además debemos informarnos dando lectura al texto “Conociendo el área y el volumen de prismas y pirámides”, el cual lo encontrarás en la sección “Recursos para mi aprendizaje”.
Continuamos trabajando teniendo en cuenta que el diseño de la estructura debe ser proporcional con las medidas reales; es decir, debes mantener las diferencias en las medidas que existen en el modelo original.
1. Iniciemos esta fase diseñando la base de la estructura de la edificación; para ello, completamos la tabla con un dibujo de las figuras geométricas que corresponda con las respectivas medidas que se consideraron en el inicio de esta actividad.
2. A continuación, completamos la siguiente tabla dibujando el boceto del cuerpo de la estructura de la edificación.
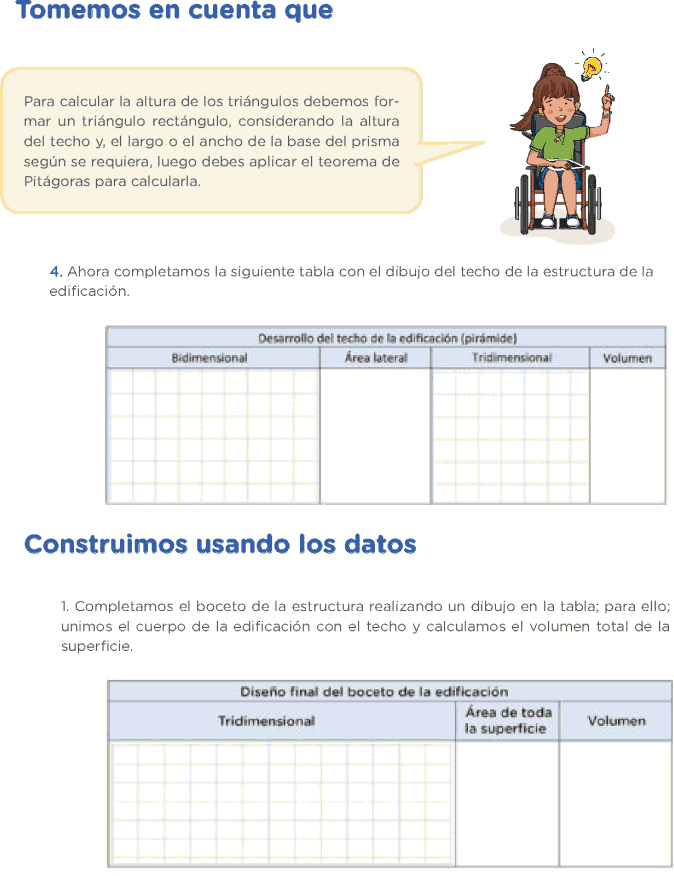
3. Enseguida, dibujemos el boceto del techo; para ello, podemos completar la tabla dibujando las figuras planas que correspondan con sus medidas: Registra en tu cuaderno de trabajo Tomemos en cuenta que
4. Ahora completamos la siguiente tabla con el dibujo del techo de la estructura de la edificación.
CONSTRUIMOS USANDO LOS DATOS
Completamos el boceto de la estructura realizando un dibujo en la tabla; para ello; unimos el cuerpo de la edificación con el techo y calculamos el volumen total de la superficie.
Ahora, respondamos en el cuaderno las siguientes preguntas:
¿Cuántos metros cuadrados de pared se necesitará en la edificación?
¿Qué cantidad de calamina, como mínimo, se requerirá para techar la construcción?
¿Qué espacio ocupará toda la estructura?
¿Qué poliedros empleamos en el diseño?
Planteamos nuestra propuesta
Finalmente, presentamos en una hoja o en el Smart Office el boceto final de la estructura.
En el debes colocar el desarrollo bidimensional del techo y cuerpo de la edificación, así como su vista tridimensional.
Evaluamos nuestros avances
Competencia:
Resuelve problemas de forma, movimiento y localización
Aprendizajes de mi actividad
Lo logré
Estoy en proceso de lograrlo
¿Qué puedo hacer para mejorar mis aprendizajes? Realicé gráficos en el plano de prismas o pirámides. Identifiqué los elementos que tienen los prismas o pirámides.
Empleé estrategias para calcular el área lateral, total y volumen del prisma y la pirámide.
Planteé relaciones entre las áreas de las figuras planas con el área lateral y total del prisma y la pirámide.
Vamos a la siguiente actividad
¡Muy bien!
Hemos culminado la actividad. Logramos diseñar la estructura de la edificación usando prismas y pirámides , que representa la propuesta para dar solución a la problemática de un asunto público que hemos observado en tu comunidad.
En la próxima actividad diseñaremos y elaboraremos composta casera como una alternativa de solución.
¡Sigue adelante!
CONOCIENDO EL ÁREA Y EL VOLUMEN DE PRISMAS Y PIRÁMIDES
Para poder determinar el área de la superficie o el volumen de un prisma o pirámide es necesario que recordemos algunos contenidos matemáticos.
Área de figuras geométricas poligonales:
El siguiente cuadro muestra las fórmulas para calcular el área de la región encerrada por una figura geométrica:
Figura Gráfico Área Triángulo
b: Longitud de la base
h: Longitud de la altura Triángulo equilatero
L: Longitud del lado Cuadrado
L: Longitud de lado Rectangulo
a: Longitud de altura b: Longitud de base
P: Perimetro de poligono ap: Longitud de apotema
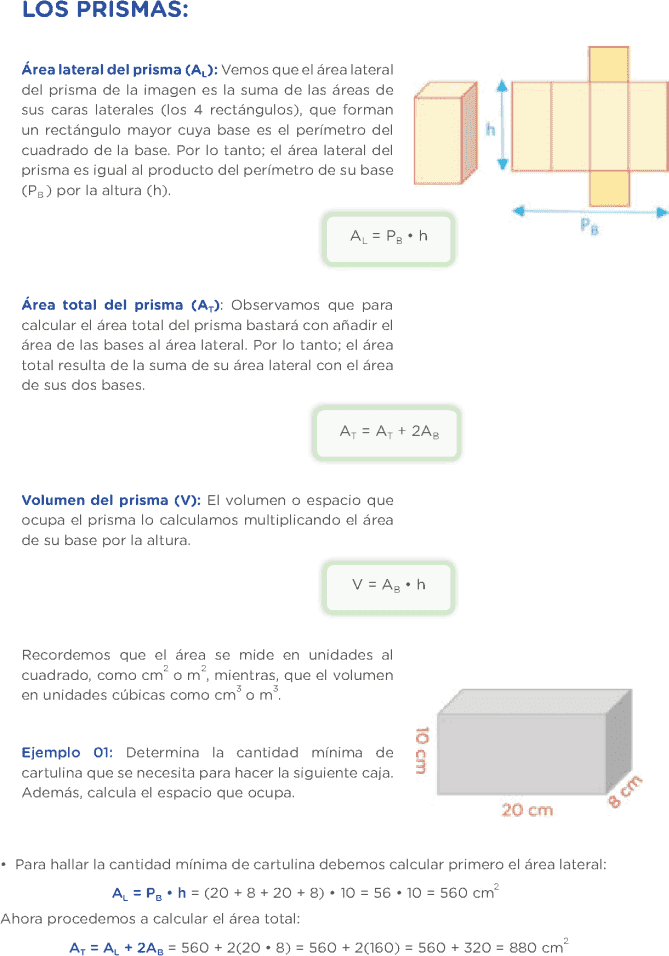
LOS PRISMAS: ÁREA LATERAL DEL PRISMA (AL):
Vemos que el área lateral del prisma de la imagen es la suma de las áreas de sus caras laterales (los 4 rectángulos), que forman un rectángulo mayor cuya base es el perímetro del cuadrado de la base.
Por lo tanto; el área lateral del prisma es igual al producto del perímetro de su base (PB ) por la altura (h).
ÁREA TOTAL DEL PRISMA (AT):
Observamos que para calcular el área total del prisma bastará con añadir el área de las bases al área lateral. Por lo tanto; el área total resulta de la suma de su área lateral con el área de sus dos bases.
VOLUMEN DEL PRISMA (V):
El volumen o espacio que ocupa el prisma lo calculamos multiplicando el área de su base por la altura.
Recordemos que el área se mide en unidades al cuadrado, como cm o m , mientras, que el volumen en unidades cúbicas como cm o m .
Ejemplo 01:
Determina la cantidad mínima de cartulina que se necesita para hacer la siguiente caja. Además, calcula el espacio que ocupa.
• Para hallar la cantidad mínima de cartulina debemos calcular primero el área lateral: Ahora procedemos a calcular el área total:
• Para calcular el espacio que ocupa la caja debemos hallar su volumen:
Damos respuesta al problema indicando que la cantidad mínima de cartulina que se necesita para construir la caja es de 880 cm y el espacio que ocupa es de 1600 cm .
LAS PIRÁMIDES:
Área lateral del prisma (AL):
Vemos que el área lateral de la pirámide de la imagen es la suma de las áreas de sus caras laterales (los 4 triángulos isósceles congruentes).
Por lo tanto; el área lateral es igual al producto del perímetro de su base (PB) por la apotema (AP) dividido entre dos.
ÁREA LATERAL DE LA PIRÁMIDE IRREGULAR (AL):
En este caso vemos, que los triángulos que forman la cara lateral no son todos congruentes. Por lo tanto; podemos afirmar que para calcular su área lateral solo debemos sumar las áreas de estos triángulos. AL = Suma de las áreas de las caras
ÁREA TOTAL DE LA PIRÁMIDE (AT):
Observamos que para calcular el área total de las pirámides anteriores bastará con añadir el área de la base al área lateral. Por lo tanto; el área total es igual a la suma de su área lateral con el de su base.
VOLUMEN DE LA PIRÁMIDE (V):
El volumen o espacio que ocupa la pirámide es igual a un tercio del producto del área de la base por la altura prismas y pirámides
EJEMPLO 02:
Calcula la cantidad mínima de papel que se necesita para envolver la vela, además halla la de cera usada para su elaboración.
• Primero debemos calcular la apotema NP, para ello realizamos un corte imaginario en la pirámide y obtenemos el triángulo rectángulo NQP, como se muestra en la imagen.
A continuación, hallamos la apotema aplicando el teorema de Pitágoras en el triángulo rectángulo NQP.
• Para hallar la cantidad mínima de papel debemos calcular primero el área lateral: Ahora procedemos a calcular el área total: